Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором меньший отрезок так относится к большему, как больший ко всему.

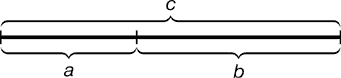
a : b = b : c или с : b = b : а.

Эта пропорция равна: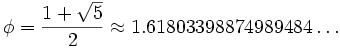

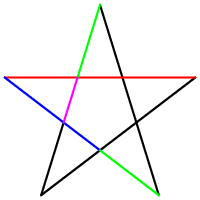
К примеру, в правильной пятиконечной звезде (сразу вспоминается Первомай), каждый сегмент делится пересекающим его сегментом в золотом сечении (т. е. отношение синего отрезка к зелёному, красного к синему, зелёного к к фиолетовому, равны 1.618

Принято считать, что понятие о золотом сечении ввел в научный обиход Пифагор. Есть предположение, что Пифагор свое знание позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования».
Цейзинг измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон.

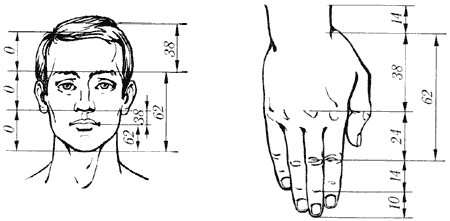
Золотые пропорции в частях тела человека                 

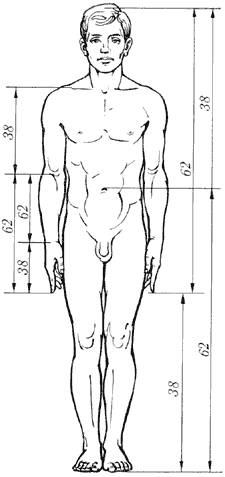
Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6.

У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской.
Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры.

Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи.

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления.

Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. (или 1.618, если делить большее число на меньшее).

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого сечения.

Золотое сечение в искусстве

Еще в 1925 году искусствовед Л.Л.Сабанеев, проанализировав 1770 музыкальных произведений 42 авторов, показал, что подавляющее большинство выдающихся сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения.

Причем, чем талантливее композитор, тем в большем количестве его произведений найдено золотых сечений. У Аренского, Бетховена, Бородина, Гайдна, Моцарта, Скрябина, Шопена и Шуберта золотые сечения найдены в 90% всех произведений. По мнению Сабанеева, золотое сечение приводит к впечатлению особой стройности музыкального сочинения.

В кино С. Эйзенштейн искусственно построил фильм Броненосец Потёмкин по правилам «золотого сечения». Он разбил ленту на пять частей. В первых трёх действие разворачивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения.

Золотое сечение в архитектуре, скульптуре, живописи

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

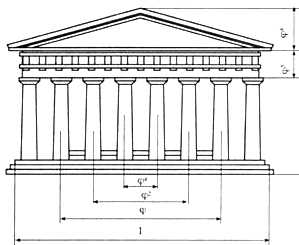
На рисунках виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618...

На плане пола Парфенона также можно заметить "золотые прямоугольники":

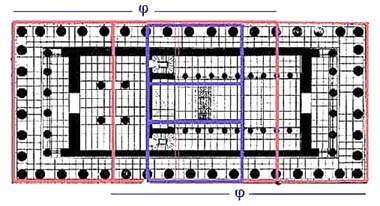
Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари), и в пирамиде Хеопса:

Не только египетские пирамиды построены в соответствии с совеpшенными пpопоpциями золотого сечения; то же самое явление обнаружено и у мексиканских пиpамид.

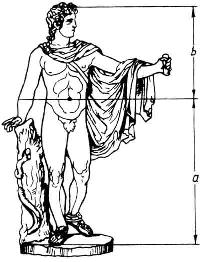
Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображенного человека делится пупочной линией в золотом сечении.

Золотое сечение в шрифтах и бытовых предметах

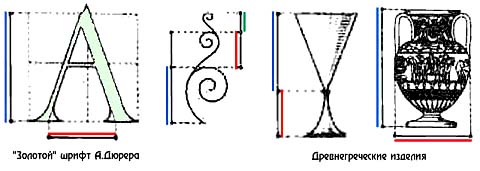
Золотое сечение в живой природе

В биологических исследованиях было показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.

Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, напр. 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи.

Хорошо известна "золотая" пропорция пятилепестковых цветков яблони, груши и многих других растений. Носители генетического кода - молекулы ДНК и РНК - имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи.

Гете подчеркивал тенденцию природы к спиральности.

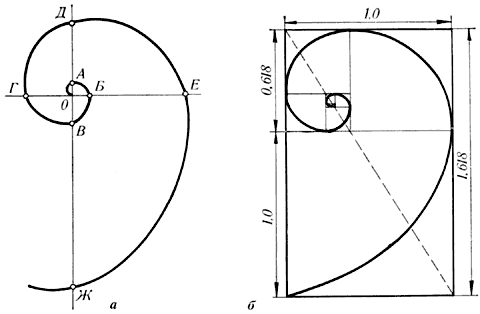
Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали.

Гете называл спираль "кривой жизни". Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д.

Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках "упакованы" по логарифмическим ("золотым") спиралям, завивающимся навстречу друг другу, причем числа "правых "и "левых" спиралей всегда относятся друг к другу, как соседние числа Фибоначчи.

Рассмотрим побег цикория. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс.

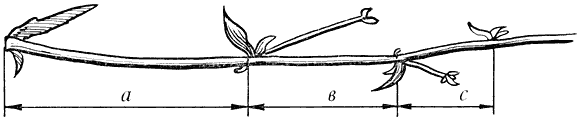
Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

У многих бабочек соотношение размеров грудной и брюшной части тела отвечает золотой пропорции. Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2,3,5,8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.

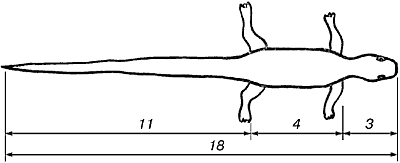
В ящерице длина ее хвоста так относится к длине остального тела, как 62 к 38. Можно заметить золотые пропорции, если внимательно посмотреть на яйцо птицы.